Paquete de Actividades Comunitarias del Día de Pi
SÁBADO, 14 DE MARZO DE 2026
Un conjunto de actividades que se pueden realizar en un grupo comunitario o en un entorno familiar, con jóvenes o adultos. Imprima el PDF aquí.
Bienvenidos/as al Paquete de Actividades Comunitarias del Día de Pi 2026!
Este año, el Día de Pi, sábado 14 de marzo de 2026, se celebrará como parte de unainiciativa anual de la división de Ciencia, Sociedad y Cultura de la Simons Foundation llamada Infinite Sums (Sumas Infinitas). La iniciativa invita a personas de todo el país a reconectarse con las matemáticas de maneras alegres, creativas y significativas. El centro de este esfuerzo es la comunidad: personas que se reúnen para explorar cómo las matemáticas se manifiestan en la vida cotidiana, desde los ritmos de la música hasta los espirales de la naturaleza, desde la narración de cuentos hasta el movimiento, y más.
Ya seas bibliotecario/a, educador/a, cuidador/a, dueño/a de un negocio local o simplemente un miembro curioso de la comunidad, este paquete de actividades se creó para ayudarte a organizar celebraciones atractivas e inclusivas para el Día de Pi. No necesitas ser un experto/a en matemáticas para participar. Solo trae tu curiosidad y deja que la experiencia te sorprenda.
Cada actividad de este paquete ofrece un vistazo único a la idea de las sumas infinitas: la adición sin fin de pequeñas partes que se unen para crear algo más grande, más rico y más complejo. Estas actividades resaltan como pasos simples, sea que involucren números, formas, palabras o acciones, pueden revelar patrones y conexiones que van más allá de lo que podemos ver inmediatamente.
Las actividades están diseñadas para ser flexibles, lúdicas y accesibles. Invitan a que personas de todas las edades, intereses y orígenes exploren las matemáticas en formas divertidas y significativas. Pueden ser usadas en bibliotecas, centros comunitarios, salones de clase, festivales o incluso en casa, y funcionan bien para grupos de todos los tamaños, o para personas que deseen hacerlas por sí mismas.
Te animamos a que conectes estas actividades a lo que más importa en tu comunidad. Eso puede incluir tu cultura, experiencias vividas o tus pasiones personales. Cuando celebres, comparte tus momentos, creaciones y descubrimientos del Día de Pi en redes sociales y usa #InfiniteSums.
Celebremos juntos, y descubramos la belleza y las maravillas de las sumas infinitas en el mundo que nos rodea.
¿Por qué Pi?
Todos los años, el 14 de marzo (o 3/14), personas en todo el mundo celebran el Día de Pi. La fecha coincide con los primeros tres dígitos de pi, 3.14. Pi es una constante matemática que aparece cada vez que mides un círculo. ¡Además también se celebra el cumpleaños de Albert Einstein, lo que hace el día más divertido!
Pero pi no es solo sobre números. Una vez que prestas atención, lo verás por todos lados. Está en las curvas de una taza de café, los anillos de un árbol, los diseños de los edificios y las trayectorias de los planetas. Artistas, ingenieros, científicos y escritores han encontrado formas de usar pi en sus obras. Nos ayuda a explorar formas, patrones y la forma en que el mundo encaja.
El Día de Pi es una oportunidad para detenernos y darnos cuenta de los círculos, espirales y ciclos que nos rodean. Es una invitación para ver como las matemáticas se conectan con la naturaleza, la creatividad y con la forma en la que nos movemos a través del espacio y tiempo.
Este paquete de actividades está lleno de maneras de explorar esas ideas. Aquí encontrarás actividades que incluyen manualidades, juegos creativos, narraciones y conversaciones que te harán pensar. Así estés planeando un evento público o solo reunir a algunos amigos en la mesa, estas actividades están diseñadas para despertar la curiosidad e invitar al descubrimiento.
Las matemáticas no sólo son fórmulas o respuestas correctas. También se tratan de maravillas, patrones y encontrar conexiones en lugares inesperados. El Día de Pi es un momento excelente para celebrar todo esto.
Comienza Aquí: Dándole Vida al Día de Pi (y a las Matemáticas)
Las matemáticas pueden sentirse intimidantes y, para muchos, el solo hecho de ver números genera estrés o ansiedad. Esos sentimientos son reales, pero el potencial para cambiarlos también lo es. La confianza en las matemáticas se nutre en espacios donde la curiosidad es bienvenida, las preguntas son alentadas y los errores son parte del camino. Ya sea que organices una celebración del Día de Pi, dirijas un grupo o reúnas a amigos y familiares, esta guía te ayudará a crear un ambiente lúdico y amistoso.
El Día de Pi es una oportunidad perfecta para hacer que las matemáticas se sientan vivas, relevantes y alegres. Es un chance para explorarlas más allá de las paredes del salón de clases, a través de historias, resolución creativa de problemas y conexiones comunitarias. Desde la repostería hasta la arquitectura, desde la agricultura hasta el diseño, las matemáticas están en todos lados. Al invitar a otros a compartir sus experiencias, estás ayudando a revelar las distintas maneras en las que las matemáticas le dan forma a nuestro mundo.
Usa esta guía como un punto de partida, no un guion. Adáptala libremente para que encaje con el rango de edad, orígenes e intereses de tu grupo. Ya sea que estés planeando actividades prácticas, organizando una charla con un orador invitado o fomentando conversaciones informales, tu energía y curiosidad marcarán la pauta.
Unos Tips Antes de Comenzar:
- – Haz pruebas. Prueba las actividades por ti mismo/a primero para saber cómo fluyen, tener ejemplos para explicarlas y determinar cuánto tiempo necesitarán los participantes./li>
- – ¡Hazlo divertido! Las matemáticas cobran vida con movimientos, historias, creatividad y experiencias compartidas.
- – Celebra las preguntas. Preguntarte “¿por qué?” o “¿qué pasaría si…?” es exactamente el punto.
- – Sé flexible. No necesitas seguir todos los pasos o completar todas las actividades. ¡Ve a donde la energía te lleve!
- – Incluye a personas reales. Invita a ponentes o voluntarios que compartan como las matemáticas están presentes en su trabajo o vidas cotidianas, y crea espacio para diversos puntos de vista.
- – Involúcrate, no actúes. Enfócate en la participación y el descubrimiento, no en tener la razón o memorizar el contenido
- – Mantente curioso/a.No necesitas todas las respuestas. Explora y aprende junto a otros.
- – Toma tu tiempo. Si una idea te genera felicidad o un interés profundo, explórala. Eso es un aprendizaje significativo.
- – Usa pi como una entrada. Está bien si las personas se van con más preguntas que respuestas.
Y, sobre todas las cosas: ¡haz que estas actividades se sientan como tuyas!
Actividad 1: Pi y Poesía con Patrones (π-ku)
Objetivo de la exploración:
Los participantes explorarán cómo los dígitos de pi pueden ser transformados en patrones de palabras y ritmos. Invita a los participantes a crear poemas en cualquier idioma y descubrir que las matemáticas tienen ritmo, belleza y espacio para la creatividad, sin requerir ecuaciones.
Descripción general:
Las sumas infinitas se extienden hasta el infinito, como los dígitos de pi o el ritmo de un poema. Los poetas y matemáticos por igual se han sentido fascinados por el infinito, el ritmo y los patrones ocultos. En esta actividad, los participantes escribirán poemas cortos llamados pi-kus.
Estos poemas siguen la forma de un haiku, pero en lugar del patrón 5-7-5 de los haiku, las sílabas de un pi-ku siguen el número de dígitos de pi (3-1-4…). Es una actividad perfecta para bibliotecas, grupos de escritura y mentes curiosas de todo tipo. Es especialmente ideal para cualquier persona que haya dicho “no me gustan las matemáticas”.

Conceptos matemáticos:
reconocimiento de patrones, razonamiento simbólico, secuencias y números irracionales
Tiempo:
20-35 minutos
Materiales:
Prepara con anticipación:
- – Opcional: imprime ejemplos de poemas pi-ku (página 9)
- – Opcional: imprime un banco de palabras para niños pequeños (página 11)
Lo que necesitarás:
- – Papel o diarios
- – Bolígrafos, marcadores o lápices
- – Opcional: una pizarra o una cuerda con pinzas para mostrar los poemas
Instrucciones (paso a paso)::
1. Presenta a pi con el contexto de la actividad. “Hoy jugaremos con las matemáticas y la poesía: usaremos el número pi como inspiración para escribir poemas cortos”. Explica que pi (3.14159…) tiene infinitos dígitos decimales que no se repiten y se encuentran en todos los círculos. Comparte un dato curioso: pi se ha calculado hasta 300 billones de dígitos decimales, y nunca se repite. ¡También puedes mostrar un visual de los dígitos de pi o mostrarlos en forma de círculo para despertar la curiosidad!
2. Explica la forma del pi-ku. “Usaremos los dígitos de pi como el patrón de nuestros poemas. La primera línea tendrá 3 sílabas, la segunda línea una sílaba y la tercera línea cuatro sílabas. ¡Eso es un pi-ku!”. La actividad puede continuar con una, cinco o nueve sílabas, si lo desean, o mantenerse sencilla con las tres primeras líneas. Asegúrate de hacer énfasis que cada línea corresponda con los dígitos de pi.
Muestra un ejemplo. Comparte un pi-ku que tú o un voluntario hayan creado en el momento. Por ejemplo:
– Círculos
– Que
– No tienen fin
¡Esto ayuda a que los participantes vean lo rápido que las matemáticas pueden convertise en palabras!
3. Facilita el tiempo de escritura. Dale a los participantes entre 15–20 minutos para escribir y considera ofrecer plantillas opcionales o ayudas visuales de inspiración. Incentiva la experimentación y la colaboración. ¡Los participantes pueden escribir varios pi-kus o trabajar en equipo!
4. Sugiere ideas para escribir:
– ¿A qué te recuerdan los círculos?
– ¿Dónde puedes ver pi en tu vida cotidiana?
– ¿Qué se siente pensar en el infinito?
– Si pi fuese una persona, ¿qué diría?
– Describe un mundo hecho de espirales o bucles.
Incentiva la libertad: “Tu pi-ku puede ser serio, gracioso o incluso sin sentido. ¡Todos son bienvenidos!”.
5. Comparte y exhibe. Invita a los participantes a leer sus pi-kus en voz alta o crea una galería en la que se puedan mostrar. ¡Celebra las interpretaciones originales y divertidas! “Noten como todos comenzaron con el mismo patrón, pero cada poema es único, como los dígitos de pi”.
6. ¡Extiende! Invita a los participantes a crear una “cadena de pi-ku”, en la que cada persona agrega una línea usando el siguiente dígito de pi. Acompaña los poemas con ilustraciones sencillas de círculos, espirales u otras imágenes alusivas a pi.
Adaptaciones comunitarias
Traduce la forma del “pi-ku” a distintos idiomas o alfabetos.
Para los más pequeños
- – En lugar de hacer un pi-ku con 3-1-4 sílabas, usa 3-1-4 palabras.
- – Provee bancos de palabras (círculo, girar, redondo, infinito, etc.).
- – Permíteles dibujar ilustraciones de pi alrededor de sus poemas.
Organiza un micrófono abierto de pi-kus para que las personas lean sus poemas.
Para adolescentes y adultos
- – Pétalos a extender la secuencia más allá de los primeros tres dígitos (1, 5, 9, …).
- – Experimenta con poemas grupales y colaborativos.
- – Incentiva el humor y referencias de cultura pop en sus pi-kus.
- – Explora traducciones de pi-ku en otros idiomas y tradiciones poéticas.

Actividad 2: Descubriendo Pi
Objetivo de la exploración:
Los participantes experimentarán cómo pi surge de la relación atemporal entre la circunferencia y el diámetro de un círculo. Al medir objetos circulares reales, comprobarán que siempre se necesita un poco más de tres diámetros para dar una vuelta a cualquier círculo, un descubrimiento divulgado por civilizaciones antiguas hace miles de años.
Descripción general:
En la actualidad, sabemos que pi es 3.14159…pero hace miles de años, cuando no existían las calculadoras o las computadoras, civilizaciones antiguas en Babilonia, Egipto, China y otros lugares encontraron maneras ingeniosas para aproximarse. Constructores y astrónomos por igual dependían de este número especial, que enlaza círculos de todos los tamaños. A través de la historia, personas de diferentes civilizaciones han estado fascinadas por la relación entre la circunferencia y el diámetro de un círculo. Esta razón, ahora llamada pi, es constante para todos los círculos, sin importar su tamaño.
En esta actividad, los participantes recrearán ese proceso haciendo que objetos circulares rueden a lo largo de una línea y comparando los diámetros a las circunferencias. Al igual que se observó hace mucho tiempo, podrán ver que siempre se necesitan alrededor de tres, y un poco más. Este experimento sencillo y práctico convierte una constante abstracta en algo visible, tangible y divertido, que también genera curiosidad sobre la historia del fascinante número pi.

Conceptos matemáticos:
circunferencia y diámetro, razón y proporcionalidad, medición y aproximación
Tiempo:
15–20 minutos
Materiales:
Prepara con anticipación:
- – Reúne objetos circulares (p. ej., platos, latas, tubos de cartón, rollos de cinta adhesiva, tapas de botellas, etc.).
- – Dibuja una línea recta larga en papel (al menos cuatro veces más larga que el diámetro de tu objeto
circular más grande). Hemos incluido una versión imprimible más adelante. (página 17)
Lo que necesitarás:
- – Bolígrafos, lápices o marcadores para hacer marcas en el papel y los objetos circulares
- – Reglas
- – Opcional: stickers pequeños o cinta adhesiva para marcar objetos circulares.
Instrucciones (paso a paso):
1. Prepara la(s) línea(s). Las usaremos para medir y marcar las circunferencias de tus objetos circulares. Usa la línea de la plantilla imprimible en papel tamaño carta para objetos pequeños, o una línea dibujada en una superficie más grande (como el suelo) para objetos más grandes. Esta será la guía para hacer rodar los círculos.
– Para un grupo con muchos participantes, se le podría entregar a cada uno una plantilla con una línea impresa luego de que les expliques la actividad. Cada participante también deberá tener un bolígrafo/lápiz/marcador para marcar la circunferencia y diámetro de su objeto en la línea.
– Escoge un objeto circular para hacer una demostración.
2. Presenta la actividad. “¿Cómo los matemáticos pudieron calcular la constante matemática pi hace miles de años? ¡Hoy descubriremos pi nosotros mismos!”
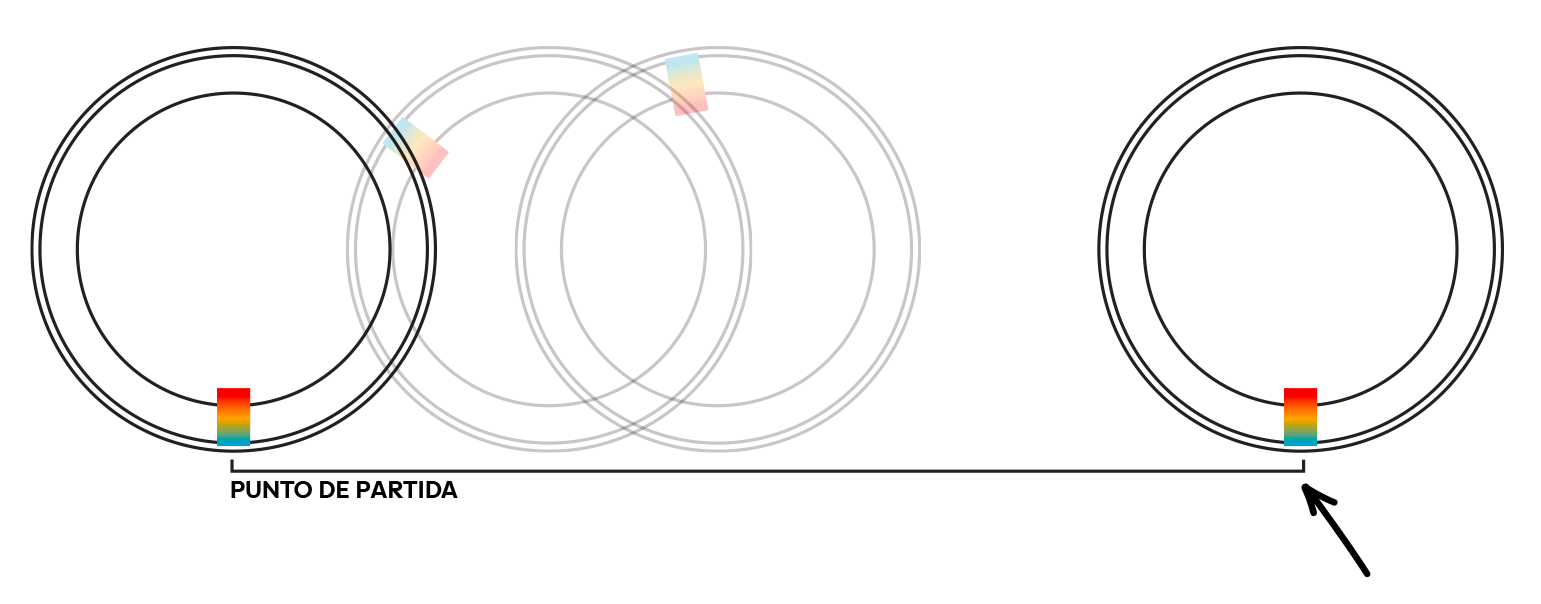
3. Marca un punto de partida. Pon un sticker, cinta adhesiva o marca en el borde de tu objeto circular. Muéstrales a los participantes cómo hacer una pequeña marca en borde de su objeto como punto de partida.

4. Rueda una revolución completa. Posiciona el objeto circular en la línea
de manera que su borde la toque, y que la marca que hecha en el paso anterior esté alineada con el inicio de la línea. Rueda lentamente el objeto por la línea hasta que la marca la toque nuevamente. Marca este unto en la línea: ¡esta es la circunferencia!
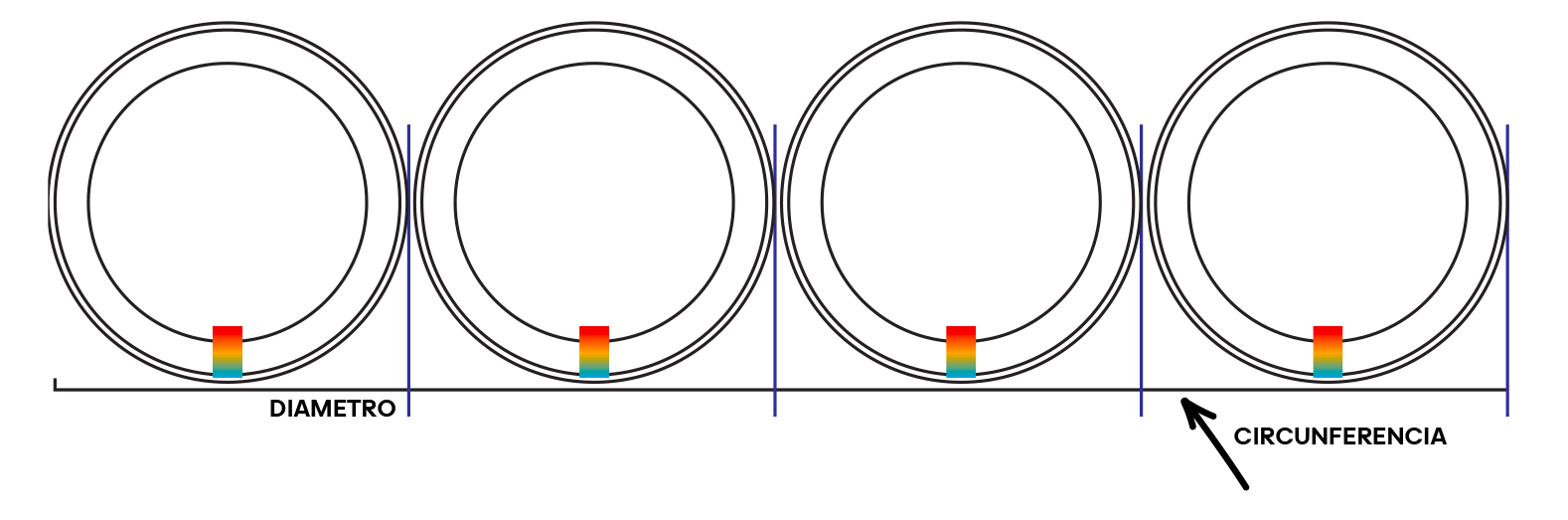
5. Mide el diámetro. Ahora coloca el objeto plano sobre la línea, con su borde tocándola. Marca la longitud de un diámetro y repite el proceso a lo largo de la línea. Cuenta cuántos diámetros caben en la circunferencia.¡Observa que la circunferencia siempre es un poco mayor que tres diámetros!
6. Repite y explora. Invita a los participantes a hacer lo mismo con diferentes círculos: tapas de botellas pequeñas, tapas de frascos medianos, platos de papel, etc. ¡Resalta como siempre funciona, sin importar el tamaño!
7. Discute y haz preguntas. “¿Por qué creen que este número era importante para tantas civilizaciones?, ¿dónde pueden ver círculos y pi en el mundo actual?”
Adaptaciones comunitarias
¡Piensa en grande! Pon un rollo de papel de manualidades en el suelo o dibuja una línea larga con tiza en un área al aire libre. Usa objetos grandescomo un aro de hula hula o un balde.
Para los más pequeños
– Para niños pequeños, enfócate en lo divertido que es hacer objetos rodar y explora la relación constante entre qué tan lejos ruedan los objetos y lo anchos que son.
– Incentiva la observación. “¿Un círculo más grande necesita rodar más?”.
Compara objetos pequeños (tapas de botellas, rollos de toallas de papel) con objetos grandes (aros de hula hula). ¡Observa como “la regla de tres o más” aplica a diferentes escalas!
Para los adolescentes
– Incluye un reto experimental: ¿quién puede aproximarse más a 3,14159… con sus mediciones? (π = circunferencia ÷ diámetro). Anímalos a medir la circunferencia y el diámetro sobre la línea con reglas y a comprobar la precisión de su aproximación al valor teórico de pi.
– Haz énfasis en la precisión (“¿Obtienen resultados similares/ consistentes al repetir las mediciones?”) y la exactitud (“¿Qué tan cerca están tus resultados de la proporción real (pi = 3,14159…)?”).
– Aliéntalos a comprobar si obtienen resultados más precisos con objetos grandes o pequeños.
Imprime varias plantillas en papel y provee varios objetos circulares para que muchas personas puedan intentar el experimento juntas.
Para los adultos
– Invítalos a reflexionar sobre cómo las culturas antiguas y modernas usan pi de forma práctica, científica, artística e inspiracional, y qué hace que esta constante sea tan fascinante universalmente.
Actividad 3: Geometría de Burbujas
Meta de la exploración:
Los participantes explorarán cómo las burbujas revelan las matemáticas en movimiento. Observarán cómo las burbujas forman esferas perfectas naturalmente, dejan huellas circulares y se encuentran en ángulos de 120 grados. A través de un juego práctico y observación, los participantes descubrirán como la naturaleza tiene un balance de belleza y eficiencias en las formas más simples.
Descripción general:
Las burbujas no solo son divertidas, ¡son matemáticas que puedes ver y tocar! Toda burbuja que flota libremente siempre forma de manera natural una esfera: la forma matemáticamente más eficiente para encerrar espacio. Cada vez que describimos el tamaño de una esfera, pi es parte de la ecuación. Desde la curvatura de una burbuja hasta la geometría de los planetas, pi nos ayuda a encontrarle sentido a las formas redondas de la naturaleza. Y cuando una burbuja se explota, deja un círculo, una “sombra” 2D de la esfera, que demuestra cómo se conectan las formas en diferentes dimensiones.
Como una exploración extra, cuando dos o más burbujas se encuentran, sus superficies jabonosas siempre se unen en ángulos de aproximadamente 120 grados (lo que forma patrones que se ven divertidos pero son guiados por la geometría), al igual que los panales, la espuma y otras estructuras naturales. Son una demostración perfecta de cómo la naturaleza “escoge” estructuras matemáticamente eficientes. Esta actividad transforma el juego en un descubrimiento matemático y genera fascinación sobre pi, la geometría y la matemática oculta en el mundo que nos rodea.

Conceptos matemáticos:
geometría de las esferas y círculos, eficiencia del área de la superficie (superficies minimales), relación entre circunferencia y diámetro, medición y estimación, geometría del círculo en sistemas físicos, ángulos formados por uniones de burbujas, patrones en estructuras naturales, matemáticas aplicadas al mundo real mediante experimentación lúdica
Tiempo:
15–25 minutos
Materiales:
Prepara con anticipación:
– Contenedores para preparar líquido para burbujas (que puedan tener al menos una taza de líquido) (uno por color)
– Para cada taza de líquido de burbujas:
– 1 taza de agua caliente
– 2 cucharadas de jabón para platos líquido (Joy o el jabón Dawn azul funcionan mejor)
– 1 cucharada de azúcar granulada (para burbujas más fuertes)
– 1 cucharada de témpera o 5 gotas de colorante para alimentos (de los colores de tu preferencia)
– Cucharas para mezclar
– Imprima la plantilla del transportador que aparece a continuación en una hoja de transparencia o papel fino de tamaño carta (página 25)
What You’ll Need:
– Varitas o popotes para hacer burbujas (idealmente, una por participante).
– Papel blanco
– Transportadores (reales o impresos)
Instrucciones (paso a paso):
1. Prepara la mezcla para burbujas. En tu contenedor designado, mezcla 1 taza de agua caliente, 2 cucharadas de jabón para platos, 1 cucharada de azúcar (esto ayudará a que las burbujas duren por más tiempo), y tu colorante a elección. Revuelve con delicadeza con una cuchara para evitar hacer espuma.
2. Prepara tu estación para hacer burbujas de forma segura. Cubre tu mesa o tu área de demostración con papel blanco para hacer las impresiones de las burbujas. Demuestra cómo sumergir un extremo del popote suavemente dentro de la mezcla, y luego soplar lenta y constantemente para formar una burbuja.
– Tip de seguridad: ¡Recuérdale a los participantes que deben soplar suavemente con el popote, no aspirar el líquido!
3. Observa las esferas. Sopla las burbujas usando el popote o la varita. Notacomo cada burbuja que flota en el aire forma una esfera tridimensional. “¿Por qué crees que las burbujas siempre se convierten en pelotas en vez de cubos o triángulos?”
– Una burbuja de jabón es simplemente una capa muy fina de agua jabonosa, llamada película de jabón, que rodea una masa de aire.
– Las burbujas siempre forman esferas (una forma de pelota) porque una esfera encierra la mayor cantidad de espacio con la menor superficie. ¡A la naturaleza le gusta la eficiencia!
4. Haz impresiones de burbujas. Deja que la burbuja caiga y explore en el papel: eso hará una impresión de la burbuja. “¿Qué forma ves en el papel?”
– Tip: Si las burbujas se están yendo con el viendo, puedes decirle a los participantes que las soplen justo por encima del papel.
5. Explora la conexión 2D-3D. “Cuando las burbujas explotan, ¿qué forma dejan en el papel?”
– Cuando las burbujas explotan, dejan marcas circulares casi perfectas. Esta marca es una “sombra” 2D circular de la esfera 3D. Esto demuestra la conexión entre 3D y 2D: ¡la redondez de la esfera se traduce en la redondez del círculo!”.
6. Opcional: explora los ángulos de las burbujas. Sopla una o más burbujas para que se toquen en el aire y deja que se exploten en el papel, para observar cómo se conectan.
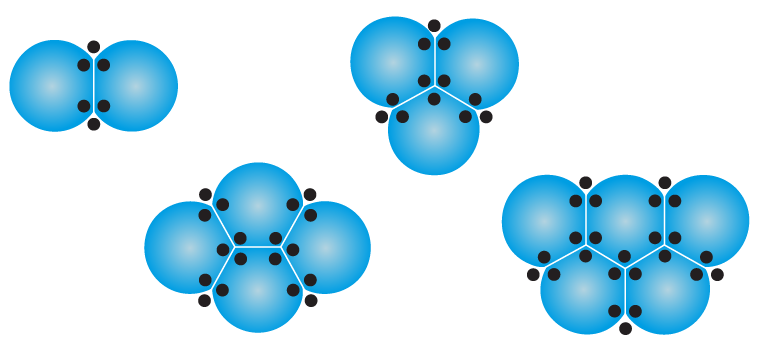
– “¿Qué notas sobre los ángulos en los que se unen las burbujas?” Cuando dos o más burbujas se juntan, las líneas en las que se unen siempre se encuentran en un ángulo de aproximadamente 120 grados.
– “¿Por qué las burbujas se unen a 120 grados?” BPorque esto minimiza el área total de la superficie. Imagina que tres superficies jabonosas se unen: si los ángulos fueran más pequeños o grandes, las superficies de las burbujas se expandirían más, lo que usaría más jabón y energía. 120 grados es el balance perfecto: cada película de jabón comparte el espacio de forma equitativa y se mantiene lo más reducida posible. La naturaleza usa este principio para ahorrar energía y materiales. ¡Por eso es que las burbujas, los panales y algunos cristales hacen esto!
– Haz la relación con otros ejemplos y conversa. conversa. “¿Pueden pensar en otros ejemplos, en la naturaleza o en la vida cotidiana, en los que las cosas se conecten de esta manera?”

¡La forma en la que las burbujas se conectan es igual a como las abejas construyen panales! En ambos casos, las líneas en las que se conectan forman ángulos de 120 grados. Esto crea patrones hexagonales, que son la manera más eficiente de conectar celdas usando la menor cantidad de material. Para las abejas, esto significa que no desperdician cera, solo usan la justa para contener la miel.

Otro ejemplo es apilar objetos: al apilar naranjas en una caja o poner baldosas en el suelo, normalmente se usan hexágonos para que encajen perfectamente.
Adaptaciones comunitarias
¡Haz un pendón de burbujas! Extiende una hoja larga de papel para manualidades e invita a los participantes a pintarlas con sus propias impresiones de burbujas coloridas y que firmen sus nombres al lado de ellas. A medida que se va llenando el pendón, se convertirá en un mural llamativo que mezcla matemáticas, arte y diversión. Una vez completado, cuélgalo en un lugar visible para que todos puedan disfrutar de esta colaboración creativa. Incluso podrías escribir los dígitos de pi en tu creación. Mientras más largo sea el pendón, más dígitos de pi podrás incluir.
Para los más pequeños
– Para niños pequeños, ¡enfócate en la diversión de las burbujas! Deja que soplen burbujas, hagan impresiones y que vean como los círculos aparecen.
– Invita a los niños a observar las formas y ángulos en los que las burbujas se unen (tienen forma de Y), sin necesidad de números.
Para los adolescentes
– Los adolescentes también pueden experimentar con burbujas de diferentes tamaños y formaciones para observar cómo cambian los patrones.
Para los adultos
– Inicia una conversación sobre cómo las películas de jabón, las burbujas y los panales representan la eficiencia y la optimización en la naturaleza. Por ejemplo, las esferas contienen la mayor cantidad de volumen con la menor área de superficie (gotas de lluvia, burbujas, planetas). Las células son aproximadamente esféricas para ahorrar espacio y energía, a su vez que contienen fluidos o nutrientes.
– Los adultos pueden enfocarse en las conexiones con la naturaleza, el diseño y la eficiencia. Por ejemplo, observar cómo la naturaleza optimiza las formas ayuda a que los ingenieros y los diseñadores ahorren material, energía y espacio. Las cúpulas geodésicas utilizan triángulos o hexágonos para delimitar espacios de forma eficiente. Diseño de embalaje: los paneles hexagonales (como los panales de las abejas) son ligeros pero resistentes. Las espumas y las estructuras similares a las burbujas inspiran materiales ligeros y aerodinámicos.
Actividad 4: Lanzamiento de Pi (Aguja de Buffon)
Meta de la exploración:
Los participantes explorarán cómo pi puede aparecer de formas sorprendentes a través de la probabilidad y los juegos. Al lanzar palillos sobre un papel con líneas y observar cuáles cruzan una línea, podrán ver patrones que surgen de las repetidas demostraciones. Los participantes descubrirán, a través de experimentos prácticos y observación, que incluso el azar puede revelar verdades matemáticas predecibles y universales.
Descripción general:
Las matemáticas a veces aparecen de las formas más inesperadas: surgen de la probabilidad y la aleatoriedad. En esta actividad, los participantes lanzarán palillos sobre papel con líneas paralelas equidistantes y observarán cuáles cruzan una línea. Tras varios lanzamientos, emergen patrones y la proporción de cruces se aproxima al valor de pi.
Este experimento clásico es conocido como el Problema de la Aguja de Buffon, en honor al matemático francés Georges-Louis Leclerc, conde de Buffon, quien lo publicó por primera vez en el siglo XVIII. Es una hermosa demostración de cómo el azar y la geometría trabajan juntos para revelar profundas verdades matemáticas. Los participantes experimentarán de primera mano cómo las pruebas repetidas y la observación cuidadosa pueden transformar eventos aparentemente aleatorios en patrones matemáticos predecibles. A través de pruebas repetidas, los participantes descubrirán que a medida que se hacen más lanzamientos, el resultado se aproxima más a pi. Esta actividad lúdica y participativa convierte un número abstracto en algo visible, tangible y divertido, y genera curiosidad sobre la probabilidad, la geometría y las sorprendentes maneras en las que las matemáticas se evidencian en el mundo.

Conceptos matemáticos:
probabilidad experimental y geométrica, proporciones y aproximación, conexión entre la geometría y la
aleatoriedad
Tiempo:
30–60 minutos
Materiales:
Prepara con anticipación:
– Hoja de papel grande o cartulina con líneas paralelas equidistantes (ver paso 1 de las instrucciones)
Lo que necesitarás:
– Regla
– Lápiz
– Palillos (o fósforos/cerillas; otros objetos largos pequeños que tengan la misma longitud)
¡Cuidado! Crea un lugar en el que sea seguro hacer los lanzamientos, especialmente si estás trabajando
con participantes más pequeños. Los palillos deben lanzarse cuidadosamente y nunca en dirección a otras
personas.
Instrucciones (paso a paso):
1. Prepare the bubble mix. In your designated container, mix 1 cup warm water, 2 tbsp dish soap, 1 tbsp a small amount of sugar (this helps bubbles last longer), and your colorant of choice. Stir gently with the spoon to avoid foam.
2. Prepara la superficie para los lanzamientos. Dibuja varias líneas paralelas (al menos cinco) en tu papel, separadas por la misma distancia. La distancia entre las líneas debe ser exactamente el doble de la longitud de los palillos (o cualquier objeto que tu grupo vaya a lanzar). Esta preparación es esencial para que la probabilidad funcione. Usa una regla para asegurarte que las medidas sean exactas.
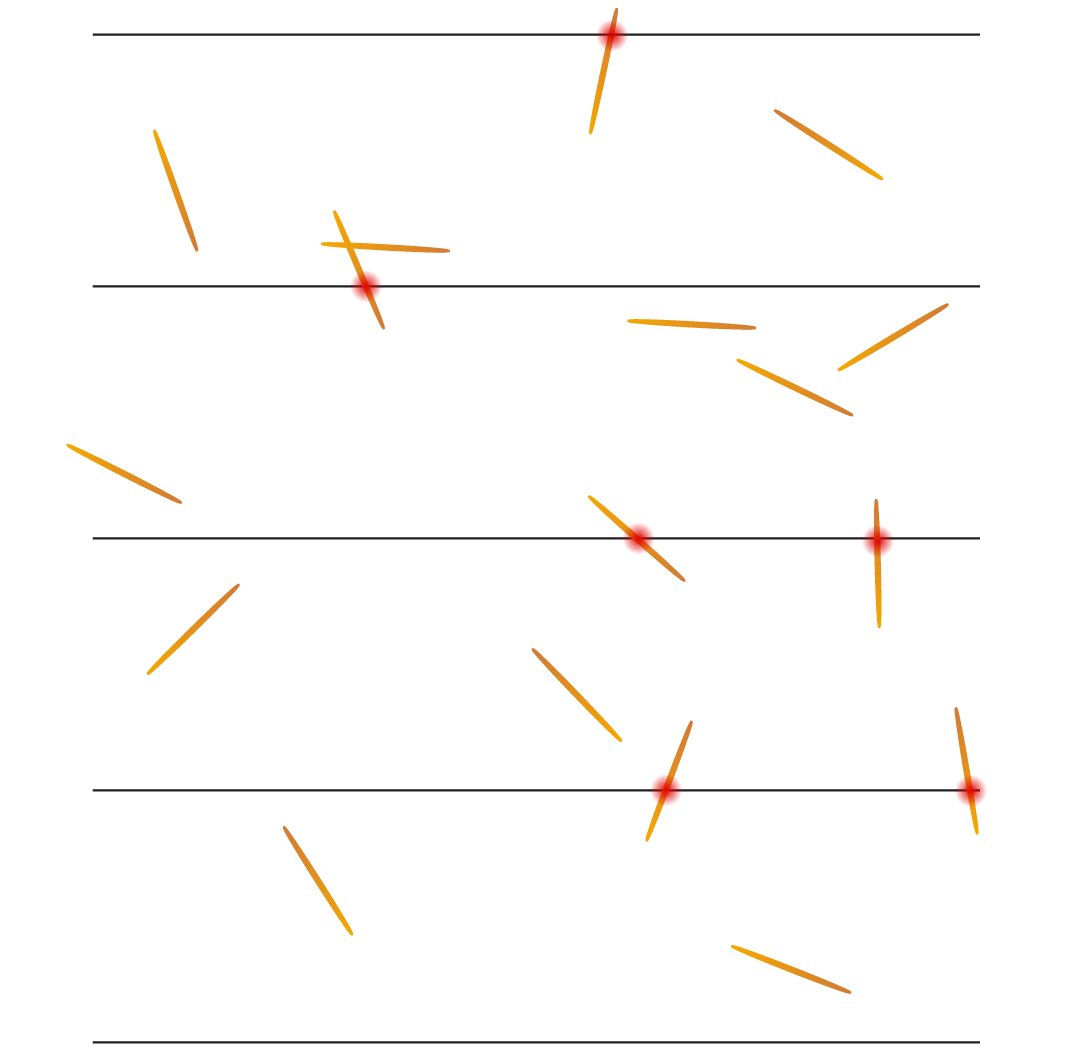
2. Lanza los palillos. “¡Vamos a lanzar palillos y ver qué tan seguido caen sobre una línea. El número pi resultará de este juego!” Entrega palillos a los participantes y deja que los lancen uno a uno sobre el papel. Invítalos a hacer lanzamientos verdaderamente aleatorios, ¡sin puntería! Permite que hagan al menos 30 lanzamientos (30 participantes lanzan un palillo o permite que los participantes lancen varios palillos cada uno hasta llegar a 30). Mientras más lanzamientos hayan, más exacta será la aproximación.
3. Cuenta y haz un registro. Luego de hacer los lanzamientos, cuenta el número total de palillos lanzados. Después cuenta cuántos de ellos cruzan o tocan una línea. Recuerda a los participantes no contar ningún palillo que caiga fuera del papel o esté por fuera del borde.
– Tip para facilitadores: Escoge un voluntario para contar el número de lanzamientos y un voluntario para contar los cruces para evitar confusiones. También puedes separar el papel en secciones y asignarlas a grupos pequeños, para luego combinar los totales.
4. Calcula pi. Usa la fórmula:

– Ejemplo: 30 lanzamientos, 10 cruces → π ≈ 30 ÷ 10 = 3.
– “¿Cuál número obtuvimos?” El resultado debe aproximarse a 3, y con más lanzamientos, se acerca más a 3.14.
5. Aumenta tu número de pruebas. Invita a los participantes a lanzar más palillos, contar, y recalcular pi repitiendo los pasos del 2 al 4. Observa como el estimado de pi calculado por el grupo se acerca más al valor real de pi con más lanzamientos.
6. Reflexiona y compara. Compara el resultado del grupo con el valor real de pi. Para muchos participantes, este es un momento revelador, al ver que pi surge del puro azar.
– “¿Cómo lanzar palillos nos dice algo sobre pi?” El hecho de que un palillo cruce una línea depende de su ángulo y dónde cae. Los ángulos son parte de un círculo, así que la geometría del círculo es naturalmente parte de la probabilidad. Cuando haces la matemática, la fórmula para la probabilidad de cruzar líneas incluye a pi.
– Resalta como la aleatoriedad, cuando se repite lo suficiente, converge con una constante universal. “¿Por qué se acerca más a pi con más lanzamientos?” La aleatoriedad se equilibra cuando se repite muchas veces (ley de los grandes números).
Adaptaciones comunitarias
¡Intenta este experimento al aire libre! Usa tiza o cinta de pintor para crear líneas paralelas anchas en el pavimento. Para una versión más grande y visible, reemplaza los palillos de dientes con palitos de helado, palillos chinos o incluso lápices. La distancia entre las líneas debe ser el doble de la longitud del palito. Por ejemplo: si los lápices miden 6 pulgadas (15 cm) de largo, separa las líneas 14 pulgadas (35 cm).
Para los más pequeños
– Concéntrate en contar y observar cuáles palillos tocan las líneas.
– Orienta la meta de la exploración hacia los giros y vueltas para aprender sobre ángulos. Pídele a los participantes que intenten: 1) dar una vuelta completa; 2) girar media vuelta para quedar de espaldas; 3) girar un poquito. “Eso es un ángulo: una forma de medir un giro. Cada giro cabe en un círculo. Si sigues girando, darás una vuelta completa, ¡y eso es un círculo!”.
Para los adolescentes
– También puedes hablar sobre porqué la aleatoriedad converge con un resultado predecible, en lo que más pruebas = más exactitud (ley de los grandes números). La ley de los grandes números dice que el resultado promedio de muchos experimentos aleatorios repetidos se aproxima cada vez más a la probabilidad real.
Para los adultos
– Con participantes adultos, explora la belleza matemática del experimento. Hablen sobre cómo esta actividad vincula la probabilidad y la geometría, y cómo surge pi de un contexto tan sorprendente.
– Este es un experimento inicial que muestra la idea detrás de los métodos actuales de Monte Carlo: utilizar la aleatoriedad para estimar respuestas cuando el cálculo directo resulta difícil.
Actividad 5: Tejidos Circulares Inspirados en Pi
Meta de la exploración:
Los participantes usarán un plato de papel como un telar para crear anillos coloridos y ver a pi en acción. Cada anillo nuevo crece en proporción a su diámetro, lo que transforma la relación abstracta entre circunferencia y diámetro en un patrón visible. Esta actividad alienta a los participantes a explorar la conexión entre matemáticas y arte mientras experimentan con colores, repetición y crecimiento.

Descripción general:
Las sumas infinitas cobran vida en los bucles y anillos del tejido, donde cada fila se construye sobre la anterior. Mediante un sencillo telar de plato de papel, los participantes experimentarán físicamente cómo los patrones repetitivos crecen y se relacionan a través de la proporción entre la circunferencia y el diámetro: el número pi. El tejido conecta las matemáticas con la creatividad sensorial, y muestra cómo la repetición de procesos puede dar lugar a una belleza tangible.
Conceptos matemáticos:
relación entre circunferencia y diámetro, geometría circular, medición y estimación, patrones y repetición
Tiempo:
20–45 minutos
Materiales:
Prepara con anticipación:
– Lanzaderas hechas con palitos de manualidades grandes o palitos de helado y estambre (ver el paso 1 de las instrucciones)
– Telares de platos de papel (ver los pasos 2–4 de las instrucciones)
– Unas cuantas copias impresas de Tejidos Circulares Inspirados en Pi (página 35 y 37)
– Un tejido con platos de papel terminado para mostrar como ejemplo
What You’ll Need:
– Paquetes de estambre de varios colores o restos de estambre que se puedan atar juntos
– Platos de papel
– Lápices
– Tijeras
– Calculadoras
– Reglas para medir y trazar líneas rectas
– Opcional: cuentas o materiales decorativos
– Opcional: tiras impresas que muestran los dígitos de pi como inspiración
¡Cuidado! Se requiere supervisión adulta si hay niños pequeños usando tijeras.
Instructions (Step-by-Step):
1. Prepara las lanzaderas de estambre. Estas se pueden preparar y repartir individualmente, o los participantes mayores pueden prepararlas en grupo. Corta el estambre en trozos de 36 a 48 pulgadas (90 a 120 centímetros). Enrolla el estambre alrededor de un palito de manualidades para evitar que se enrede (esta será la lanzadera). Opcional: Ata los trozos más cortos para crear una hebra más larga y colorida.
2. Prepara el plato de papel. Estos se pueden preparar y repartir individualmente, o los participantes mayores pueden prepararlas en grupo. En el reverso, divide el plato en un número impar de secciones con lápiz y regla (de 7 a 9 secciones para los niños pequeños, y más de 9 para los mayores). Traza líneas rectas en el reverso del plato para marcar las secciones.
3. Haz cortes en la parte superior de cada sección. Corta ranuras de 1–1.5 pulgadas (2,5 a 4 centímetros) a lo largo de las líneas dibujadas en el borde del plato, dejando intacto el espacio en el centro. Estas ranuras servirán para sujetar los radios de tu telar de plato de papel.
4. Convierte el plato de papel en un telar. Luego, muestra cómo pasar el estambre por las ranuras opuestas, atándolo firmemente por detrás. Continúa hasta que cada ranura tenga un “radio” de estambre, como una rueda de bicicleta. Ata la última pieza en el centro, tensando bien los hilos de estambre. Esto mantendrá el telar en su lugar. Recorta o esconde los extremos de los hilos.

5. Usa una lanzadera para comenzar a tejer desde el centro. Ata la lanzadera al centro del telar. Demuestra cómo tejer pasando el hilo por encima y por debajo alrededor de los radios, trabajando hacia afuera en anillos.
6. Presenta a pi en el contexto de la actividad. Explica que pi (aproximadamente 3,14) es la relación entre la circunferencia de un círculo y su diámetro. Aclara que “si se mide la circunferencia de un círculo de estambre y esa medida se divide entre la distancia que lo atraviesa, ¡la respuesta siempre será pi!”. Invita a los participantes a imaginar su tejido como un modelo físico de esta relación.
7. Añade más colores y patrones. Anima a los participantes a cambiar de lanzadera cada pocos anillos para crear capas coloridas. Reta a adolescentes y adultos a crear un tejido “codificado con pi” asignando diferentes colores a los dígitos de pi (por ejemplo, 3 anillos = azul, 1 = rojo, 4 = amarillo, etc.).
8. Conecta el tejido a pi. Una vez que los participantes tengan algunos anillos en su telar, haz una pausa y pídeles que midan la longitud del hilo, en centímetros, utilizada para un anillo completo: la circunferencia del anillo. Pídeles que comparen sus medidas con la fórmula: circunferencia = π × diámetro. Indica lo siguiente: “Cada anillo más grande requiere más hilo, ¡pi nos ayuda a calcular cuánto más!”. En otras palabras, la creciente longitud de estambre necesaria para cada nuevo anillo refleja la relación de pi entre la circunferencia y el diámetro, convirtiendo una fórmula abstracta en algo que pueden ver y medir en su tejido.
9. Compara sus resultados.. After participants have measured the yarn for a few of their rings, have them compare their results with the table included on the Circular Weavings Inspired by pi printout. Point out that while each ring’s diameter grows steadily, the amount of yarn needed increases according to pi. Encourage them to see how closely their yarn lengths match the calculated circumferences — a perfect “aha!” moment, where pi comes to life in their weaving.
10. ¡Completa y muestra los tejidos! Cuando los participantes lleguen al borde del plato, ata el estambre cuidadosamente. Muestra los tejidos terminados en una “Galería de Pi” para celebrar la matemática detrás del arte.
Adaptaciones comunitarias
Usa materiales reciclados o naturales para hacer tejidos ecológicos.
Para los más pequeños
– Prepara las lanzaderas de estambre y telares de platos de papel con anticipación para que los niños puedan comenzar a tejer.
– Permíteles usar uno o dos colores en vez de medir.
– Convierte el tejido en una actividad de contar: cuenten los anillos o radios juntos.
– Explícales que “cada nuevo anillo es más grande porque, gracias a pi, los círculos siempre crecen de la misma forma”.
Invita a artesanos locales a demostrar técnicas tradicionales de tejidos circulares.
Para los adolescentes
– Haz que los adolescentes midan, corten y enhebren sus propias lanzaderas y telares de platos de papel para practicar la simetría y el espaciado.
– Rétalos a seguir los números de pi con diferentes colores de estambre (3 = azul, 1 = rojo, 4 = amarillo).
– Pídeles que midan la circunferencia de cada anillo y la comparen con pi multiplicado por el diámetro.
Muestra los tejidos en espacios comunitarios con explicaciones sobre la matemática involucradas.
Para los adultos
– Haz que midan, corten y enhebren sus propias lanzaderas y telares de platos de papel para practicar la simetría y el espaciado.
– Invítalos a compartir sus propias historias sobre tradiciones de tejido circular (por ejemplo, cestería o atrapasueños).
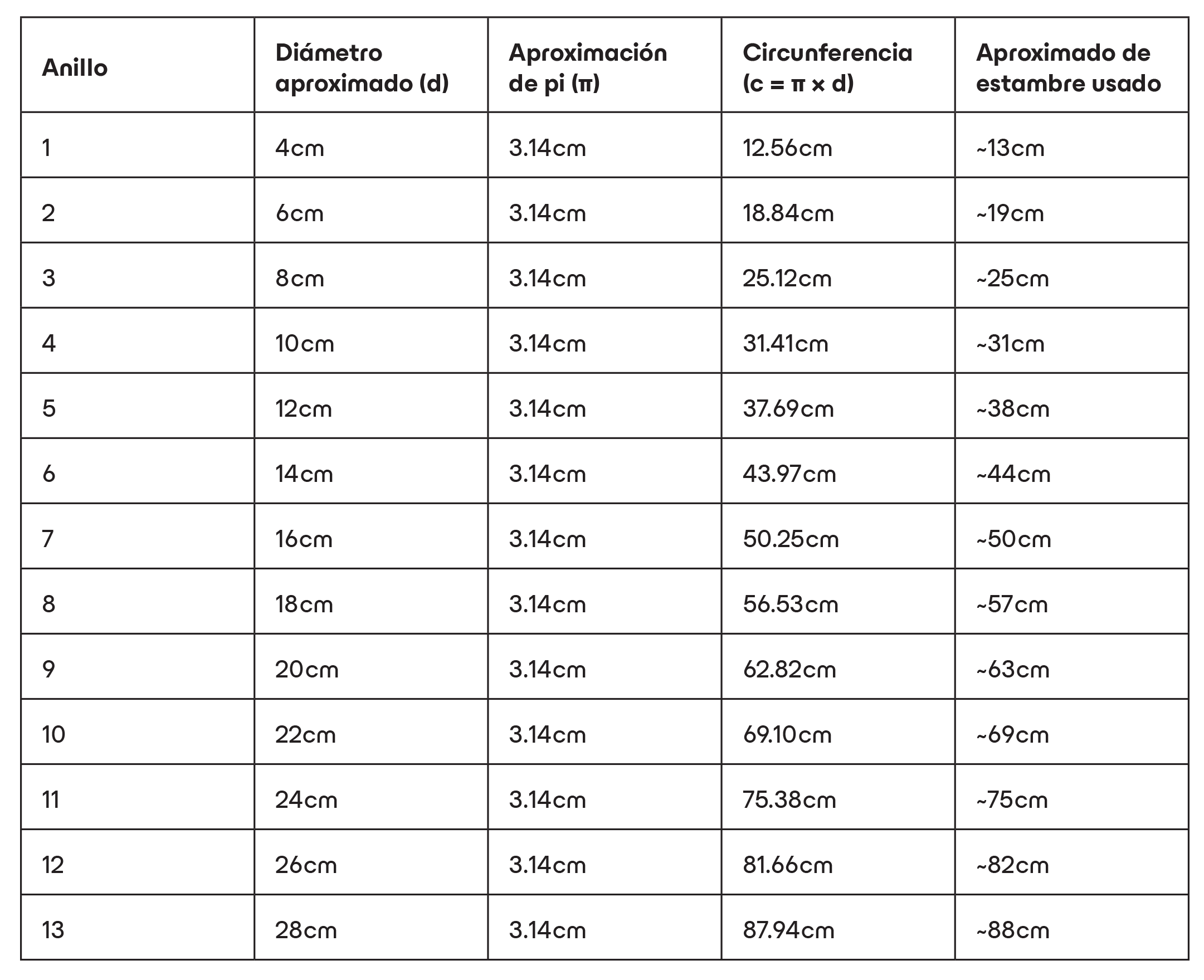
Midiendo los Anillos: Longitud del estambre y pi en acción
CÓMO LEER ESTA TABLA:
– No olvides que la circunferencia del anillo es igual a la medida del diámetro del anillo multiplicado por pi.
– La columna de “aproximado de estambre usado” nos da el estimado más cercano a lo que los participantes observarán cuando midan sus anillos.
– La columna de “circunferencia” nos muestra la longitud exacta de estambre utilizado para hacer el anillo.